Função composta

Vemos muito nas aulas de matemática a função composta. Vimos em posts anteriores função do primeiro grau, mas foi uma abordagem da função do primeiro grau simples. A função composta se caracteriza como um atalho para um terceiro conjunto. Sabemos que há dois conjuntos na função do primeiro grau, certo? vimos que para mantermos nossa função real precisamos saber quais números não podem ir no domínio da função. Como nunca podemos parar de aprender, chegou a hora de entender como funciona a função composta Vejamos antes um diagrama de função composta.

Diagrama função composta

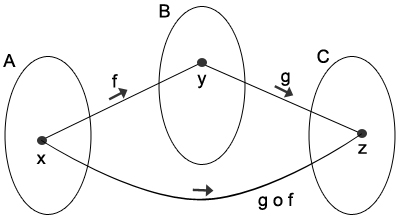
No diagrama da função composta podemos notar que é como existisse uma segunda função, no caso a função C, que é formada pelas funções A e B. Em linguagem matemática, isso significa que f: A → B e g: B → C. Agora, um "atalho" de A → C é muitas vezes vista como h: A → C que é representado como (g o f)(x).
A Simbologia: fog (x) = f(g(x)), gof (x) = g(f(x)) e fof (x) = f(f(x)).
Ainda no diagrama acima podemos notar os elementos x,y e z de cada conjunto, no caso, são indefinidos só para exemplificar.

Exemplo de função composta do primeiro grau

f(x) = 3x -1, g(x) = x², determine g(f(2)).
Neste exercício de função composta acima devemos determinar o g o f, ou em outras palavras, determinar a função composta de f: 2. Para isso vamos fazer o seguinte:
Solução do exercício de função composta:
g o f(2) = g(f(2))
Sei que f(x) = 3x -1, sei também que está definido g(f(2)), então, se eu substituir o x na função f(x) = 3x -1 terei: f(2) = 3.2 - 1 → f(2) = 5.
Opa, tenho f(2) = 5, então, vamos dar continuidade a resolução da função composta acima.
g o f(2) = g(5)
Ora, sei que g(x) = x², certo? e tenho também que g(5), então basta substituir o x por 5. temos então:
g(x) = x² → g(5) = 5² → g(5) = 25
Muito bom!, resolvemos a função composta, conseguimos determinar g(f(2)) que é 25. Dúvidas? deixe um comentário.