Algebrismo basico.

Fatoração algebrica.

Neste post estaremos vendo alguns exemplos de fatoração e finalmente estudando oque é soma, subtração, e multiplicação, e também divisão de polinomios.

Ex-1.


Ex-2.


Ex-3.


Ex-4.



Ex-5.


Agora que sabemos fatorar a^2 - b^2 podemos aprender outros casos.

Este é um polinomio que sempre temos de trabalhar.
1)

Vamos ver um exemplo deste tipo de fatoração



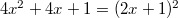
Em geral para fatorarmos um trinomio quadrado perfeito, inicialmente verificamos se o trinomio é
de fato um quadrado perfeito, para isso, é necessario fazermos algumas contas.

Vamos extrair a raiz de 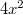e 1, temos 2x e 1.

agora verificamos se como se verifica, o trinomio é quadrado perfeito.

Deste produto notavel


podemos conseguir uma maneira mais eficiente de verificar isto.

Um trinomio do tipo acima será quadrado perfeito se sqrt(a^2)*sqrt(b^2) = 2ab
Isto é, extraimos a raiz quadrada dos monomios que figuram-se como elevados a potencia dois.
e verificamos se eles estão obedecendo aigualdade acima.

Vamos agora definir formalmente a multiplicação , divisão, e subtração de polinomios.

Subtração.

Seja f e g duas funções definidas num dominio D.
A subtração delas decorre do fato de que para toda função k(x) podemos sempre obter a função
-k(x) portanto, a subtração de f e g é expressa em termos de uma soma isto é e podemos proceder como no primeiro caso.

A multiplicação.



e a divisão



O dominio destas funções soma/multiplicção/divisão/subtração obdecem certas propriedades
mas não iremos falar sobre elas agora.